Editer Mathématiques
Sommaire
1. Opérations de base
- Poser une addition
- Poser une soustraction
- Poser une multiplication
- Poser une division
2. Règle de trois / Produit en croix
3. Nombre premiers
- Plus grand commun diviseur (PGCD)
- Plus petit commun multiple (PPCM)
4. Critères de divisibilités
5. Fractions
- Rendre une fraction irréductible
- Mettre des fractions au même dénominateur
- Addition/soustraction de fractions
- Multiplication/division de fractions
- Factorielle
- Puissances
1) On superpose les nombres à additionner en prenant soin de mettre les unités sous les unités, les dizaines sous les dizaines... On trace une ligne en dessous.
2) On commence par les unités, on les additionne et marque le résultat sous la ligne. Attention, si le résultat dépasse la dizaine, on reportera le chiffre de la dizaine sur la colonne de la dizaine (une "retenue").
3) On continue d'additionner les colonnes des dizaines, centaines, milliers... en notant et reportant si nécessaire.
1) On superpose les nombres, ce que l'on veut soustraire en dessous de celui dont on veut soustraire en prenant soin d'aligner les unités, dizaines, centaines... en colonne et on trace une ligne en dessous.
2) On commence par les unités (tout à droite). 2 cas se posent alors :
-soit le nombre du haut est plus grand que celui du bas, à ce moment là c'est facile, on fait la soustraction et on note le résultat sous le trait, aligné avec la colonne.
-si le nombre du haut est plus petit que celui du bas, il faut ajouter "10" au nombre du haut. On ajoute "10" au nombre du haut (en général on met un petit "1" devant, juste pour mémoriser qu'on l'a fait, en rouge ci-dessous) et surtout ne pas oublier d'ajouter "1" à la colonne des dizaine au nombre que l'on veut soustraire (le plus important, en vert ci-dessous). Dans l'image suivante, "4" devient "14" pour qu'on puisse y soustraire "7". 6 devient 6+1, et c'est ça qu'on devra soustraire à 12 par la suite.
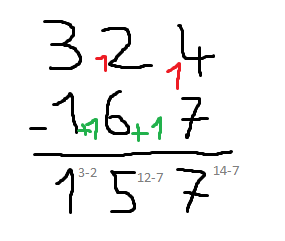
Il est important de maitriser la pose de l'addition.
1) On superpose, unités sur unités, dizaine au dessus de dizaine. On tire un trait en dessous.
2) On multiplie le chiffre des unités du nombre au dessous par le chiffre des unités du nombre au dessus. S'il dépasse la dizaine, on le marque en retenue dans la colonne dizaines. On marque le résultat sous le trait.
3) On multiplie le chiffre de la dizaine du nombre au dessous par le chiffre des dizaine du nombre au dessus. On additionne la retenue éventuellement laissée dans cette colonne par l'étape d'avant.
4) Quand on passe d'une colonne à l'autre, on écrit sous le résultat obtenu précédemment en décalant d'une unité.
5) On additionne les nombres obtenus.
Explication visuelle :
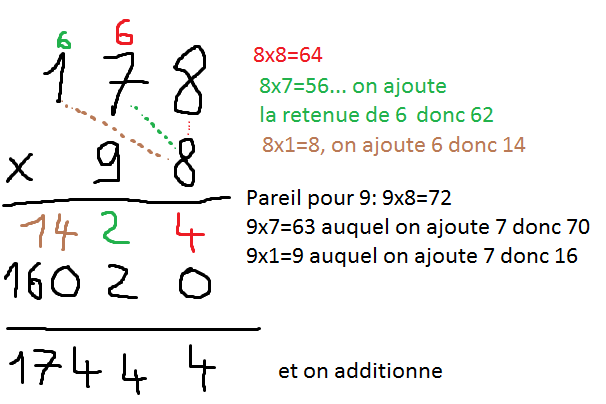
Il est important de maitriser la pose de la soustraction.
1) On place le nombre à diviser (dividende) et le nombre par lequel on va diviser (diviseur) côte à côte. On souligne le diviseur.
2) On se pose la question "combien de fois le premier chiffre du dividende contient le diviseur ?".
Par exemple, si on veut diviser 657 par 3, on voit que "6" contient 2 fois 3. Si c'est impossible (exemple 234 divisé par 5-> 2 ne contient pas 5), on met un zéro et on utilise 2 chiffres du dividende ("combien de fois 23 contient-il 5 ?").
3) On écrit le nombre de fois que l'on a trouvé sous le trait sous le diviseur.
4) On soustrait le nombre de fois*le dividende aux chiffres que l'on a utilisé. Pour reprendre l'exemple de 234 : on soustrait 4x5=20 à 23.
5)On met le chiffre suivant au côté du résultat de la soustraction. Pour reprendre l'exemple de 234 : on met à côté de 3 le 4 restant.
6)On continue.
Explication visuelle :
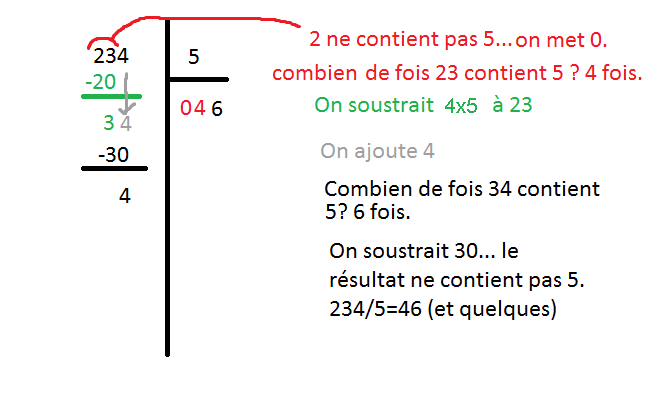
1 kilo de pomme vaut 5 euros.
2.5 vaut combien ?
D'instinct on va faire : 5*2.5 (car on passe de 1€ à 2.5 en multipliant par 2.5).
La logique fonctionne avec d'autres nombres :
40 divisé par 12 pour trouver le prix au kg. Puis on multiplie par 24 pour trouver le prix de 24kg.
Un nombre est premier quand il n'est divisible que par 1 et lui même. Tous les nombres qui ne sont pas premiers sont décomposables en nombres premiers.
Pour décomposer en nombre premier, on essaie de diviser le nombre par 2. Si ça ne marche pas, on passe à 3, siça ne fonctionne pas 5, etc.
Liste minimum à retenir : 2, 3, 5, 7, 11, 13, 17.
Exemple :
96=48*2=24*2*2=12*2*2*2=6*2*2*2*2=3*2*2*2*2*2
Autre exemple (on voit qu'au début on ne peut pas diviser par 2 ou 3 donc on doit utiliser 5) :
1875=375*5=75*5*5=15*5*5*5=3*5*5*5*5
Attention, certains nombres sont peu décomposables, par exemple :
1886=2*23*41
En décomposant plusieurs nombre, on peut trouver le plus grand diviseur qu'ils ont en commun.
Par exemple :
24=12*2=6*2*2=3*2*2*2
84=42*2=21*2*2=7*3*2*2
On retrouve ici 2*2*3, soit 12 en commun. 24 est divisible par 12 et donne 12, 84 est divisible par 12 et donne 7.
Bonnes explications et exercices
Un multiple est le produit d'un nombre avec n'importe quel autre (entier naturel). 9 est un multiple de 3. 8734 est un multiple de 2.
Le plus petit commun multiple correspond au plus petit multiple partagé par 2 nombres. Par exemple, le plus petit commun multiple de 12 et 20 est 60.
On peut le voir lorsqu'on essaye tous les multiples de ces nombres :
...
12*4=48
12*5=60
12*6=72
...
...
20*2=40
20*3=60
20*4=80
...
Plutôt que d'essayer de multiplier (ce qui peut être très long), on peut aussi factoriser en nombres premiers.
12=2*2*3
20=2*2*5
Puis on "combine" en les multipliant les chiffres identiques sans changer le maximum de fois où ils apparaissent dans chaque nombre. Par exemple "2" apparait 2 fois au maximum, on écrira 2*2. 3 et 5 apparaissent une fois, on les utilisera tous les 2.
Ce qui donne : 2*2*3*5=60
Autre exemple :
18=2*3*3
30=2*3*5
2*3*3*5=90
Pareil pour 3 nombres :
8=2*2*2
9=3*3
12=2*2*3
2 apparait 3 fois maximum, 3 apparait 2 fois maximum. On fait donc 2*2*2*3*3 soit 72.
En fait, c'est logique : on garde les diviseurs communs aux 2 nombres et on y multiplie les diviseurs différents.
Afin de ne pas faire des divisions inutiles lors de factorisation, il est utile de savoir quelques astuces.
Voir aussi :
Les nombres rationnels sont ceux qui peuvent être exprimés sous forme de fraction. Une fraction se compose de deux nombres séparés par un trait : au dessus se trouve le numérateur, en dessous est le dénominateur. Si on divise le numérateur par le dénominateur on obtient la forme décimale (exemple : 16/8 donne 2 en forme décimale). Il est intéressant d'utiliser des fractions car sous cette forme elles peuvent exprimer des nombres impossibles à noter en forme décimale (3/14).
Le numérateur peut être un chiffre négatif (mais pas le dénominateur, on ne peut pas diviser par un chiffre négatif). Parfois, on met le signe "-" devant toute la fraction.
Si on multiplie le numérateur et le dénominateur par le même nombre, la fraction ne change pas (16/8 vaut 32/16).
"Simplifier" une fraction, c'est diviser son numérateur et son dénominateur par le même nombre (16/8 peut se simplifier en 8/4 si on divise par 2). Lorsqu'on ne peut plus diviser une fraction (sauf par 1 vu que tout peu se diviser par 1), on dit qu'elle est irréductible.
Il suffit de trouver le plus grand commun diviseur (PGCD) au numérateur et au dénominateur, puis de les diviser avec, pour rendre une fraction irréductible.
Exemple :
-60/144
-On décompose 60 : 3*5*2*2
-On décompose 144 : 3*3*2*2*2*2
-On trouve 3*2*2 en commun. Leur plus grand diviseur commun est donc 12.
-60 divisé par 12 : 5.
-144 divisé par 12 : 12.
-60/144 est donc 5/12 en forme irréductible.
Pour mettre des fractions au même dénominateur (afin de les manipuler et les comprendre plus facilement), il suffit de multiplier la fraction avec le dénominateur de l'autre.
Exemple :
-On veut mettre 4/9 et 2/5 avec le même dénominateur.
-4*5/9*5 et 2*9/5*9.
-Ce qui donne 20/45 et 18/45.
On peut aussi choisir de les multiplier par le plus petit multiple commun.
Exemple :
-On veut mettre 4/15 et 5/21 avec le même dénominateur. On pourrait faire 4*21/15*21 et 5*15/21*15 (ce qui donnerait 84/315 et 75/315) mais on va essayer de les simplifier en même temps.
-On décompose 15=3*5, 21=7*3.
-On trouve le plus petit multiple commun avec la technique vue plus haut : 3*5*7=105.
-On trouve un moyen de mettre 105 au dénominateur en le multipliant (ici, 15*7 et 21*5).
-On multiplie le numérateur de la même façon (4*7 et 5*5).
-Résultat, 4/15 et 5/21 donnent 44/105 et 28/105.
Il suffit de les mettre au même dénominateur et d'additionner les numérateurs.
Exemple :
1/3+1/4=4/12+3/12=7/12
C'est la même chose pour une soustraction.
Simple, on multiplie les numérateurs entre eux et les dénominateurs entre eux.
2/3*5/7=2*5/3*7=10/21
Pour la division, il faut inverser le numérateur et le dénominateur de la fraction par laquelle on veut diviser, puis multiplier les fractions entre elles :
2/3 : 5/7=2/3*7/5=14/15
La factorielle d'un nombre est le produit des nombres entier positifs inférieur ou égaux à ce nombre.
Exemple :
La factorielle de 8 est 1*2*3*4*5*6*7*8=40320
C'est utile pour savoir combien de combinaisons différentes il peut y avoir si on ne doit pas réutiliser les éléments formant la combinaison.
Par exemple, pour les éléments ABC, il y a 6 combinaisons possibles : ABC,ACB,BAC,BCA,CAB,CBA
On peut le calculer avec la factorielle de 3 : 1*2*3=6
Bonnes infos
La puissance se note par un petit chiffre en haut à droite d'un nombre (ou séparé d'un ^). S'il est positif, on multiplie le nombre par lui même autant de fois que la puissance.
Exemple :
3²=3*3=27
3^2=3*3=27
Si la puissance de n'importe quel nombre est de zéro, on considère que le résultat est 1 :
3^0=1
Si la puissance de n'importe quel nombre est de 1, on considère que le résultat ne change pas.
3^1=3
Si une puissance est négative, on considère qu'il indique le nombre, avec une puissance positive, comme dénominateur avec un comme numérateur.
3
Pour multiplier un chiffre avec le même avec une puissance différente, il suffit d'additionner les puissances :
3
Pour diviser un chiffre avec le même avec une puissance différente, il suffit de soustraire les puissances :
3
Pour trouver la puissance d'un chiffre déjà avec une puissance, il faut les multiplier :
(3
Si une puissance est appliquée à une fraction, elle est appliquée au dénominateur et au numérateur.
(2/3)
Ajouter une puissance à 0 n'a pas de sens et donnera zéro.
1. Opérations de base
- Poser une addition
- Poser une soustraction
- Poser une multiplication
- Poser une division
2. Règle de trois / Produit en croix
3. Nombre premiers
- Plus grand commun diviseur (PGCD)
- Plus petit commun multiple (PPCM)
4. Critères de divisibilités
5. Fractions
- Rendre une fraction irréductible
- Mettre des fractions au même dénominateur
- Addition/soustraction de fractions
- Multiplication/division de fractions
- Factorielle
- Puissances
Opérations de base
Poser une addition
1) On superpose les nombres à additionner en prenant soin de mettre les unités sous les unités, les dizaines sous les dizaines... On trace une ligne en dessous.
2) On commence par les unités, on les additionne et marque le résultat sous la ligne. Attention, si le résultat dépasse la dizaine, on reportera le chiffre de la dizaine sur la colonne de la dizaine (une "retenue").
3) On continue d'additionner les colonnes des dizaines, centaines, milliers... en notant et reportant si nécessaire.
Poser une soustraction
1) On superpose les nombres, ce que l'on veut soustraire en dessous de celui dont on veut soustraire en prenant soin d'aligner les unités, dizaines, centaines... en colonne et on trace une ligne en dessous.
2) On commence par les unités (tout à droite). 2 cas se posent alors :
-soit le nombre du haut est plus grand que celui du bas, à ce moment là c'est facile, on fait la soustraction et on note le résultat sous le trait, aligné avec la colonne.
-si le nombre du haut est plus petit que celui du bas, il faut ajouter "10" au nombre du haut. On ajoute "10" au nombre du haut (en général on met un petit "1" devant, juste pour mémoriser qu'on l'a fait, en rouge ci-dessous) et surtout ne pas oublier d'ajouter "1" à la colonne des dizaine au nombre que l'on veut soustraire (le plus important, en vert ci-dessous). Dans l'image suivante, "4" devient "14" pour qu'on puisse y soustraire "7". 6 devient 6+1, et c'est ça qu'on devra soustraire à 12 par la suite.
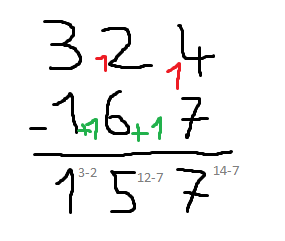
Poser une multiplication
Il est important de maitriser la pose de l'addition.
1) On superpose, unités sur unités, dizaine au dessus de dizaine. On tire un trait en dessous.
2) On multiplie le chiffre des unités du nombre au dessous par le chiffre des unités du nombre au dessus. S'il dépasse la dizaine, on le marque en retenue dans la colonne dizaines. On marque le résultat sous le trait.
3) On multiplie le chiffre de la dizaine du nombre au dessous par le chiffre des dizaine du nombre au dessus. On additionne la retenue éventuellement laissée dans cette colonne par l'étape d'avant.
4) Quand on passe d'une colonne à l'autre, on écrit sous le résultat obtenu précédemment en décalant d'une unité.
5) On additionne les nombres obtenus.
Explication visuelle :

Poser une division
Il est important de maitriser la pose de la soustraction.
1) On place le nombre à diviser (dividende) et le nombre par lequel on va diviser (diviseur) côte à côte. On souligne le diviseur.
2) On se pose la question "combien de fois le premier chiffre du dividende contient le diviseur ?".
Par exemple, si on veut diviser 657 par 3, on voit que "6" contient 2 fois 3. Si c'est impossible (exemple 234 divisé par 5-> 2 ne contient pas 5), on met un zéro et on utilise 2 chiffres du dividende ("combien de fois 23 contient-il 5 ?").
3) On écrit le nombre de fois que l'on a trouvé sous le trait sous le diviseur.
4) On soustrait le nombre de fois*le dividende aux chiffres que l'on a utilisé. Pour reprendre l'exemple de 234 : on soustrait 4x5=20 à 23.
5)On met le chiffre suivant au côté du résultat de la soustraction. Pour reprendre l'exemple de 234 : on met à côté de 3 le 4 restant.
6)On continue.
Explication visuelle :

Règle de trois / Produit en croix
1 kilo de pomme vaut 5 euros.
2.5 vaut combien ?
| Kg de pommes | Prix |
|---|---|
| 1kg | 5€ |
| 2,5kg | ?€ |
D'instinct on va faire : 5*2.5 (car on passe de 1€ à 2.5 en multipliant par 2.5).
La logique fonctionne avec d'autres nombres :
| Kg de noisettes | Prix |
|---|---|
| 12kg | 40€ |
| 24kg | ?€ |
40 divisé par 12 pour trouver le prix au kg. Puis on multiplie par 24 pour trouver le prix de 24kg.
Nombre premiers
Un nombre est premier quand il n'est divisible que par 1 et lui même. Tous les nombres qui ne sont pas premiers sont décomposables en nombres premiers.
Pour décomposer en nombre premier, on essaie de diviser le nombre par 2. Si ça ne marche pas, on passe à 3, siça ne fonctionne pas 5, etc.
Liste minimum à retenir : 2, 3, 5, 7, 11, 13, 17.
Exemple :
96=48*2=24*2*2=12*2*2*2=6*2*2*2*2=3*2*2*2*2*2
Autre exemple (on voit qu'au début on ne peut pas diviser par 2 ou 3 donc on doit utiliser 5) :
1875=375*5=75*5*5=15*5*5*5=3*5*5*5*5
Attention, certains nombres sont peu décomposables, par exemple :
1886=2*23*41
Plus grand commun diviseur (PGCD)
En décomposant plusieurs nombre, on peut trouver le plus grand diviseur qu'ils ont en commun.
Par exemple :
24=12*2=6*2*2=3*2*2*2
84=42*2=21*2*2=7*3*2*2
On retrouve ici 2*2*3, soit 12 en commun. 24 est divisible par 12 et donne 12, 84 est divisible par 12 et donne 7.
Plus petit commun multiple (PPCM)
Bonnes explications et exercices
Un multiple est le produit d'un nombre avec n'importe quel autre (entier naturel). 9 est un multiple de 3. 8734 est un multiple de 2.
Le plus petit commun multiple correspond au plus petit multiple partagé par 2 nombres. Par exemple, le plus petit commun multiple de 12 et 20 est 60.
On peut le voir lorsqu'on essaye tous les multiples de ces nombres :
...
12*4=48
12*5=60
12*6=72
...
...
20*2=40
20*3=60
20*4=80
...
Plutôt que d'essayer de multiplier (ce qui peut être très long), on peut aussi factoriser en nombres premiers.
12=2*2*3
20=2*2*5
Puis on "combine" en les multipliant les chiffres identiques sans changer le maximum de fois où ils apparaissent dans chaque nombre. Par exemple "2" apparait 2 fois au maximum, on écrira 2*2. 3 et 5 apparaissent une fois, on les utilisera tous les 2.
Ce qui donne : 2*2*3*5=60
Autre exemple :
18=2*3*3
30=2*3*5
2*3*3*5=90
Pareil pour 3 nombres :
8=2*2*2
9=3*3
12=2*2*3
2 apparait 3 fois maximum, 3 apparait 2 fois maximum. On fait donc 2*2*2*3*3 soit 72.
En fait, c'est logique : on garde les diviseurs communs aux 2 nombres et on y multiplie les diviseurs différents.
Critères de divisibilités
Afin de ne pas faire des divisions inutiles lors de factorisation, il est utile de savoir quelques astuces.
Voir aussi :
| Divisible par | Si.... |
|---|---|
| 2 | Le nombre est pair. |
| 3 | La somme des chiffres du nombre est divisible par 3. |
| 4 | Les 2 chiffres de droites sont un multiple de 4. |
| 5 | Le chiffre se termine par 0 ou 5. |
| 6 | Divisible par 2 ET par 3. |
| 8 | Les 2 chiffres de droites sont un multiple de 8. |
| 9 | La somme des chiffres du nombre est un multiple de 9. |
| 10 | Le dernier chiffre est 0. |
| 11 | "la différence entre la somme des chiffres de rang pair et la somme des chiffres de rang impair est un multiple de 11" source |
| 25 | Le nombre se termine par 00, 25, 50 ou 75. |
| 100 | Le nombre se termine par 00. |
Fractions
Les nombres rationnels sont ceux qui peuvent être exprimés sous forme de fraction. Une fraction se compose de deux nombres séparés par un trait : au dessus se trouve le numérateur, en dessous est le dénominateur. Si on divise le numérateur par le dénominateur on obtient la forme décimale (exemple : 16/8 donne 2 en forme décimale). Il est intéressant d'utiliser des fractions car sous cette forme elles peuvent exprimer des nombres impossibles à noter en forme décimale (3/14).
Le numérateur peut être un chiffre négatif (mais pas le dénominateur, on ne peut pas diviser par un chiffre négatif). Parfois, on met le signe "-" devant toute la fraction.
Si on multiplie le numérateur et le dénominateur par le même nombre, la fraction ne change pas (16/8 vaut 32/16).
"Simplifier" une fraction, c'est diviser son numérateur et son dénominateur par le même nombre (16/8 peut se simplifier en 8/4 si on divise par 2). Lorsqu'on ne peut plus diviser une fraction (sauf par 1 vu que tout peu se diviser par 1), on dit qu'elle est irréductible.
Rendre une fraction irréductible
Il suffit de trouver le plus grand commun diviseur (PGCD) au numérateur et au dénominateur, puis de les diviser avec, pour rendre une fraction irréductible.
Exemple :
-60/144
-On décompose 60 : 3*5*2*2
-On décompose 144 : 3*3*2*2*2*2
-On trouve 3*2*2 en commun. Leur plus grand diviseur commun est donc 12.
-60 divisé par 12 : 5.
-144 divisé par 12 : 12.
-60/144 est donc 5/12 en forme irréductible.
Mettre des fractions au même dénominateur
Pour mettre des fractions au même dénominateur (afin de les manipuler et les comprendre plus facilement), il suffit de multiplier la fraction avec le dénominateur de l'autre.
Exemple :
-On veut mettre 4/9 et 2/5 avec le même dénominateur.
-4*5/9*5 et 2*9/5*9.
-Ce qui donne 20/45 et 18/45.
On peut aussi choisir de les multiplier par le plus petit multiple commun.
Exemple :
-On veut mettre 4/15 et 5/21 avec le même dénominateur. On pourrait faire 4*21/15*21 et 5*15/21*15 (ce qui donnerait 84/315 et 75/315) mais on va essayer de les simplifier en même temps.
-On décompose 15=3*5, 21=7*3.
-On trouve le plus petit multiple commun avec la technique vue plus haut : 3*5*7=105.
-On trouve un moyen de mettre 105 au dénominateur en le multipliant (ici, 15*7 et 21*5).
-On multiplie le numérateur de la même façon (4*7 et 5*5).
-Résultat, 4/15 et 5/21 donnent 44/105 et 28/105.
Addition/soustraction de fractions
Il suffit de les mettre au même dénominateur et d'additionner les numérateurs.
Exemple :
1/3+1/4=4/12+3/12=7/12
C'est la même chose pour une soustraction.
Multiplication/division de fractions
Simple, on multiplie les numérateurs entre eux et les dénominateurs entre eux.
2/3*5/7=2*5/3*7=10/21
Pour la division, il faut inverser le numérateur et le dénominateur de la fraction par laquelle on veut diviser, puis multiplier les fractions entre elles :
2/3 : 5/7=2/3*7/5=14/15
Factorielle
La factorielle d'un nombre est le produit des nombres entier positifs inférieur ou égaux à ce nombre.
Exemple :
La factorielle de 8 est 1*2*3*4*5*6*7*8=40320
C'est utile pour savoir combien de combinaisons différentes il peut y avoir si on ne doit pas réutiliser les éléments formant la combinaison.
Par exemple, pour les éléments ABC, il y a 6 combinaisons possibles : ABC,ACB,BAC,BCA,CAB,CBA
On peut le calculer avec la factorielle de 3 : 1*2*3=6
Puissances
Bonnes infos
La puissance se note par un petit chiffre en haut à droite d'un nombre (ou séparé d'un ^). S'il est positif, on multiplie le nombre par lui même autant de fois que la puissance.
Exemple :
3²=3*3=27
3^2=3*3=27
Si la puissance de n'importe quel nombre est de zéro, on considère que le résultat est 1 :
3^0=1
Si la puissance de n'importe quel nombre est de 1, on considère que le résultat ne change pas.
3^1=3
Si une puissance est négative, on considère qu'il indique le nombre, avec une puissance positive, comme dénominateur avec un comme numérateur.
3
| -3=1/3 | 3 |
|---|
Pour multiplier un chiffre avec le même avec une puissance différente, il suffit d'additionner les puissances :
3
| 2 * 3 | 4=3 |
|---|
Pour diviser un chiffre avec le même avec une puissance différente, il suffit de soustraire les puissances :
3
| 2 : 3 | 5=3 | <
|---|
Pour trouver la puissance d'un chiffre déjà avec une puissance, il faut les multiplier :
(3
| 3 | 2) | 3=3 | 2*3=3 |
|---|
Si une puissance est appliquée à une fraction, elle est appliquée au dénominateur et au numérateur.
(2/3)
| 2/3) | 2=(2 | 2/3 |
|---|
Ajouter une puissance à 0 n'a pas de sens et donnera zéro.